|
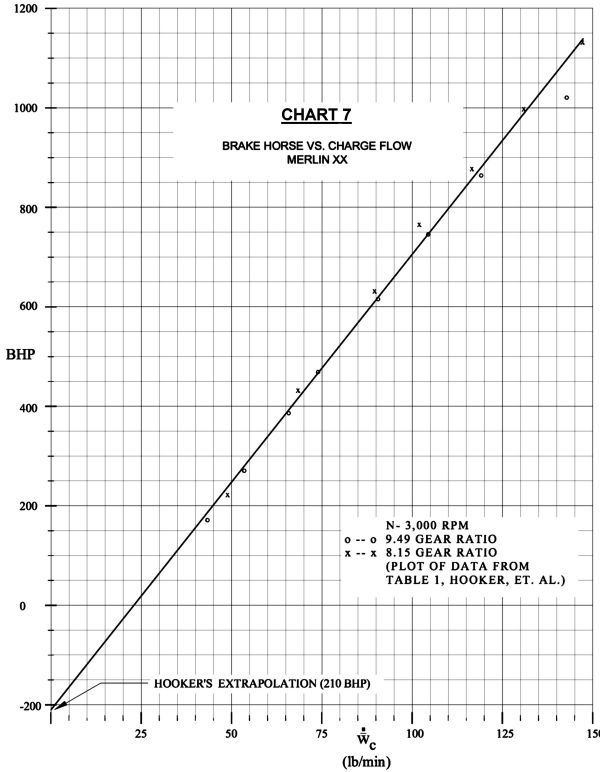
1. Hooker, S., Reed, H., and Yarker, A., The Performance of a Supercharged Aero Engine, Technical Series No. 3, Rolls-Royce Heritage Trust, P.O. Box 31, Derby, Great Britain, DE24 8BJ.
2. Hooker, Stanley (Sir), Not Much of an Engineer, SAE Press, 1984.
3. Raymond, R. J., “A Comparison of Sleeve Valve and Poppet Valve Aircraft Piston Engines “, April, 2005, Aircraft Engine Historical Society web site, www.enginehistory.org
4. Taylor, C.F., The Internal Combustion Engine in Theory and Practice, Vol. 1,
M.I.T. Press.
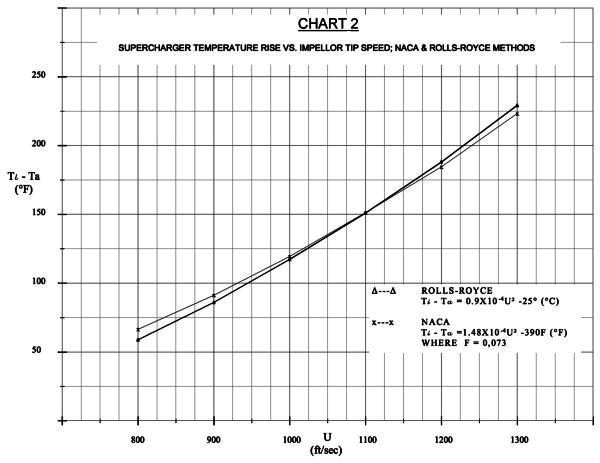
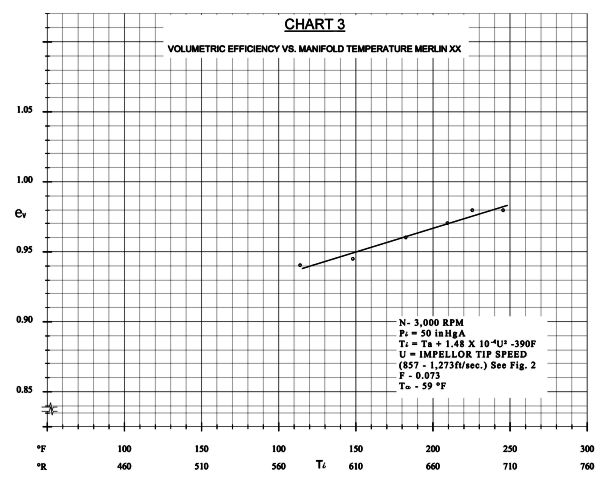
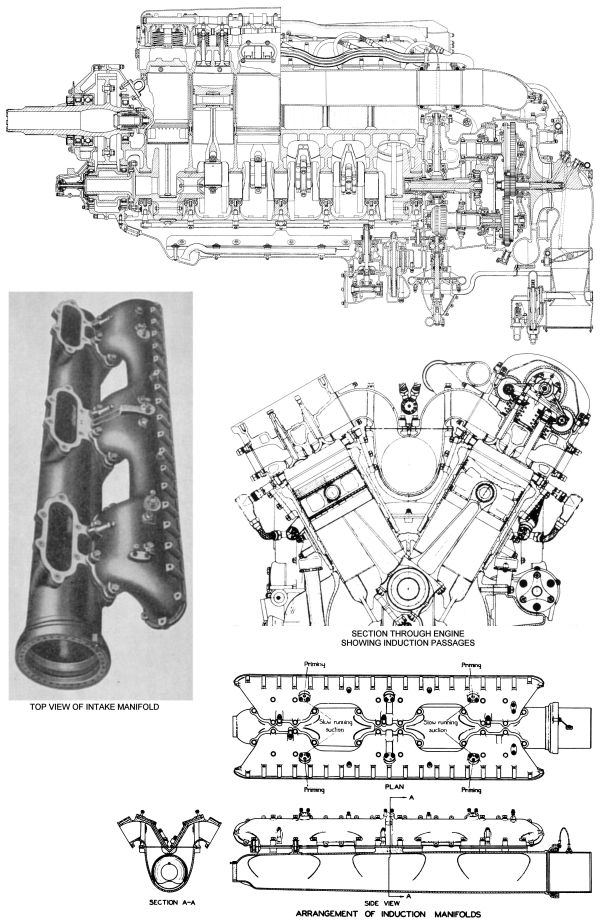
5. White, J.H., and Gammon, G.L., “Correlation of Mixture Temperature Data Obtained from Bare Intake-Manifold Thermocouples“, NACA MR No. E5L03, January, 1946.
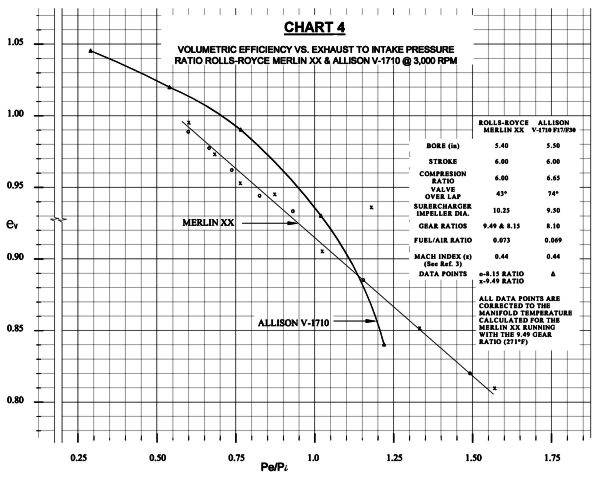
6. Desmon, L.G., and Doyle, R.B., “Effect of Exhaust Pressure on the Performance of a 12-Cylinder Liquid Cooled Engine“, NACA TN 1367,
May 1947.
7. Taylor, et.al., “Dynamics of the Inlet System of a Four-Stroke Single-Cylinder Engine” , ASME Transactions 77, Oct., 1955, p.1133
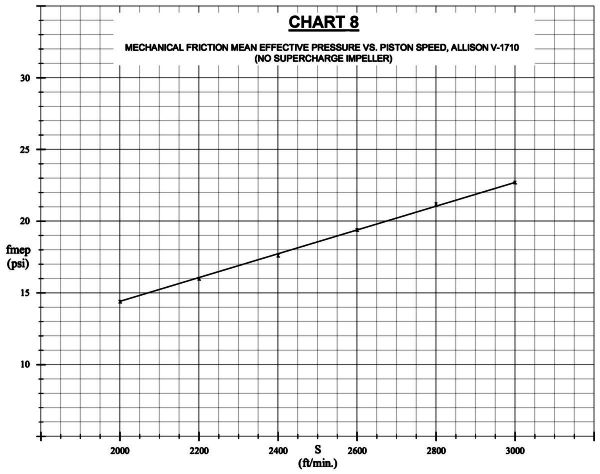
8. Allison Test Report A2-7, NASM file D52.41/64. Figure 1, “Engine Friction & Air Horsepower, Allison V-1710 “F” Engine”
|
9. Bishop, I.N., “Effect of Design Variables on Friction and Economy”, SAE Paper 812A, Automotive Engineering Congress, Jan., 1964.
10. Campbell, K. and Talbot, J., “Some Advantages and Limitations of Centrifugal and Axial Compressors”, SAE Journal (Transactions),
Vol. 53, No. 10, Oct., 1945.
11. NACA Subcommittee on Supercharger Compressors, “Standard Procedures for Rating and Testing Centrifugal Compressors“,
NACA ARR No. E5 F13, June 13, 1945.
12. Schlaifer and Heron, Development of Aircraft Engines and Fuels, Harvard University Graduate School of Business Administration, Cambridge MA, 1950.
13. Reference 4, Figure 5-12.
14. Edson and Taylor, “The Limits of Engine Performance—Comparison of Actual and Theoretical Cycles “, Contained in SAE Publication TP-7, Digital Calculations of Engine Cycles, 1964.
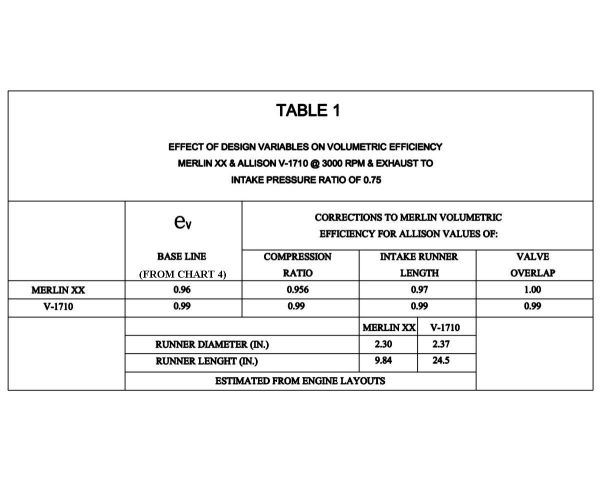
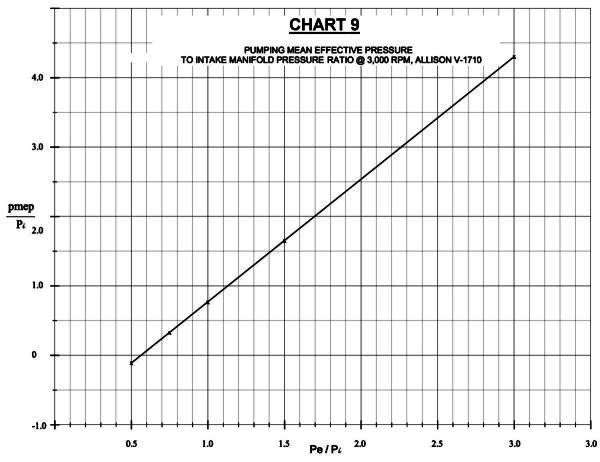
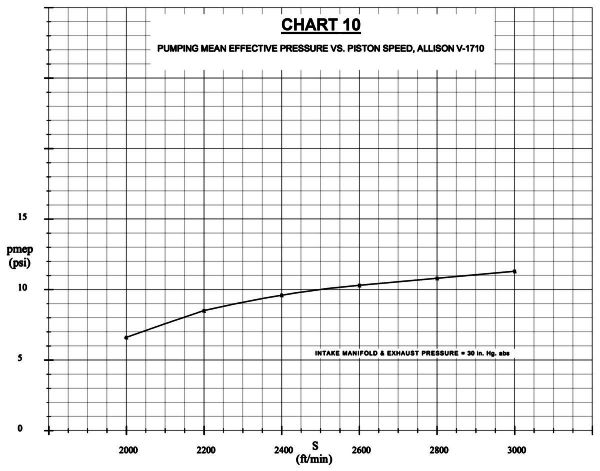
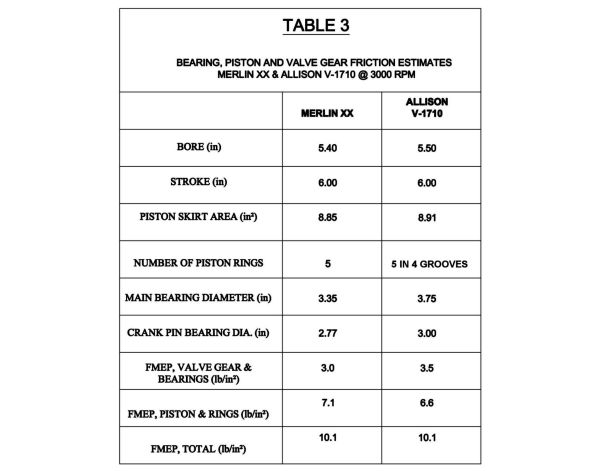
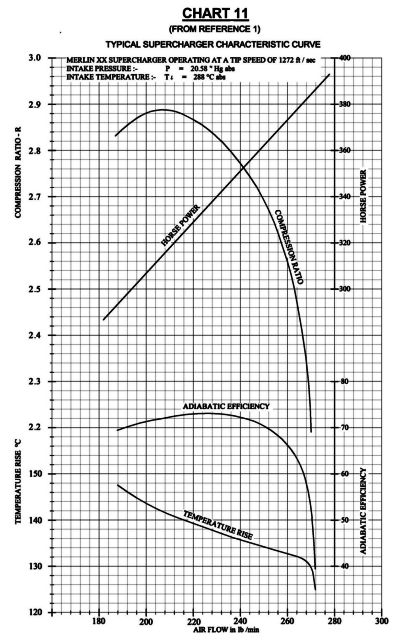
The method for calculating mean effective pressure is explained in the author’s earlier paper “Comparison of Sleeve and Poppet-Valve Aircraft Piston Engines.”
|
![]() – charge flow, air plus fuel
– charge flow, air plus fuel![]() – fuel flow
– fuel flow![]() – air flow
– air flow![]() – choking mass flow
– choking mass flow![]()