

Engine Power Calculators
Compiled by Kimble D. McCutcheon
Published 31 Aug 2017; Revised 10 Sep 2017
The Use of the Pratt & Whitney Aircraft Power Calculator
(P&WA OI 63)
Purpose
The power calculator is a simplified power curve. For the specific engine and the particular operating conditions for which the card is drawn, it shows the relation between brake horsepower (bhp), absolute manifold pressure, rpm, and pressure altitude; and it also supplies the data necessary to correct the first two of these quantities for changes in carburetor air temperature (c.a.t.). In particular, it is designed to provide a means of estimating rapidly, under flight conditions, and with an accuracy sufficient for practical purposes, two important quantities, namely:
1. Engine power output (bhp) from the observed readings of four instruments, the manifold pressure gauge, tachometer, altimeter, and c.a.t. gauge;
2. Manifold pressure required to deliver a desired bhp at a given altitude, rpm, and c.a.t.
Incorporated in many of the calculator cards is a bmep chart, to assist the operator in selecting economical rpm-bhp combinations and avoiding those that result in excessive bmeps.
Description
The following description is based on power calculator, P&WA 1943 PC 5, R-2000 2SDG, using the Low Blower, Auto-Lean Operation Side.
Slide and Case
The calculator consists of a cardboard slide and its transparent plastic case. On each face of the slide are stated the engine model and the operating conditions to which it applies (e.g., R-2000 2SDG, LOW BLOWER, 140 BMEP, AUTO-LEAN). It is essential that the appropriate slide and the proper side of the slide be used in making the computations. The cases are all identical, and may be used with any of the slides.
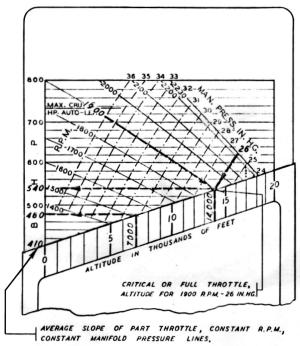
Example 2: bhp delivered by a given rpm - manifold pressure combination (1,900 rpm, 26 inHgA) at various altitudes.
An operator wishes to compute the bhp delivered at several different altitudes by a constant rpm of 1,900 and a constant manifold pressure of 26 inHgA. Locate the intersection of the full throttle 1,900 rpm and 26 inHgA lines, and through this intersection pass the sloping edge of the case. Reading from the altitude and bhp scales, the power output of the selected rpm-manifold pressure combination proves to be: at set level, 410 bhp; at 7,000 ft, 480 bhp; and at 14,000 ft (the altitude determined by the intersection of the full throttle 1,900 rpm and 26 inHgA lines), 554 bhp.
The altitude determined by the intersection of the given full throttle rpm and manifold pressure lines is the full throttle, or critical altitude for the selected rpm-manifold pressure combination. (For example: the critical altitude for 2,200 rpm - 25 inHgA is 17,000 ft). It represents the maximum altitude and power obtainable with that particular combination without ram. (With ram, both the critical altitude and the maximum power may be increased.) It throttle setting and all other conditions remain unchanged, manifold pressure increases as altitude decreases; therefore, all operation below the critical altitude must be at part throttle to maintain a constant manifold pressure.
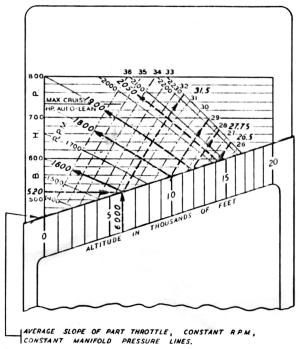
Example 3: Different rpm - manifold pressure combinations delivering a desired bhp (520) at a given altitude (6,000 ft).
An operator wishes to find the various combinations of rpm and manifold pressure that will deliver 520 bhp at 6,000 ft. Adjust the slide so that the 520 bhp, line cuts the sloping edge of the case at the 6,000 ft altitude mark. The part throttle, constant rpm, constant manifold pressure line will be found to pass through the intersection of the full throttle 1,800 rpm and 29 inHgA lines, showing that 520 bhp can be obtained at 6,000 ft by part throttle operation at 1,800 rpm and 21 inHgA manifold pressure. The same sloping line also passes through a number of other full throttle, constant rpm, constant manifold pressure line intersections. All such intersections that lie at or above 6,000 ft represent rpm-manifold pressure combinations that will deliver 520 bhp, at 6,000 ft. For example: 2,050 rpm - 26.5 inHgA; 1,900 rpm - 27.75 inHgA; and 1,600 rpm - 31.5 inHgA, the last being a full throttle combination, while all others represent part throttle operation.
Because an average constant manifold pressure anti rpm line must be used, minor errors will be introduced into the calculations, and the results obtained will differ slightly from those obtained from the corresponding power curves. It must be realized that the power calculator is primarily a time-saving, convenience and not a substitute for the more accurate power curve.
 |
 |
 |
| Example 2. BHP Delivered | Example 3. RPM/MP Combinations | Example 4. BMEP Chart |
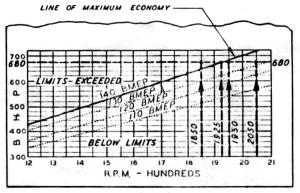
Example 4: BMEP Chart
Printed on the lower half of the slide is a modified bmep chart, designed to assist the operator in choosing an rprn. For maximum fuel and engine economy, the rpm and bhp selected should determine a point lying as close below the diagonal bmep line as possible. If the point lies above the line, the limiting bmep is being exceeded, and a higher rpm and/or a lower bhp must be selected.
Assume a bhp of 680 is desired at 5,000 ft with maximum fuel economy. Setting the slide in the same manner as in Example 3 it is found that 680 bhp is delivered at 5,000 ft by such part throttle rpm-manifold pressure combinations as: .1,850 rpm - 35 ininHgA, 1,950 rpm - 33.5 inHgA, and 2,050 rpm - 32.5 inHgA. Referring to the bmep chart, it appears that the first of these rpms is too low, since the point 1,950 rpm - 680 bhp lies above the maximum bmep line; the second rpm is close to the optimum, inasmuch as the: point 1,950 rpm-680 bhp is just below the diagonal; the third rpm is too high, resulting in an unnecessarily low bmep and wastage of fuel. As shown on the bmep chart, the most economical rpm for 680 bhp is 1,925, which corresponds to a manifold pressure of 33.75 inHgA as computed on the altitude curve.
While operation at maximum permissible bmep may result in the greatest fuel and engine economy, in practice specific airplane or propeller characteristics may call for operation below this limit. Under no circumstances, however, may the limiting bmep be exceeded without risk of damage to the engine.
On certain power calculator cards, several diagonal lines are printed on the bmep chart to enable the operator to estimate bmep, and the range of prohibited bmeps is shaded.
All other operating limitations that appear on the slide (e.g., 'Maximum Cruising Horsepower', etc.) should be noted.
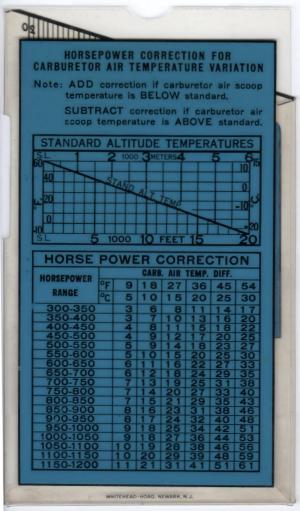
Carburetor Air Temperature Correction Tables
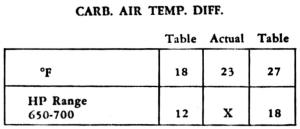 |
| Interpolation Example. Since 23 lies 5/9 of the way from 18 to 27, the actual correction, X, must be approximately 5/9 of the way from 12 to 18, in other words, 15. |
In general it will be necessary to correct all computed bhps and manifold pressures for variations of carburetor air temperatures from standard conditions. On the back of the calculator case is a table of standard altitude temperatures from sea level to 20,000 ft.
EXAMPLE 5. From this table the standard temperature at 12,500 ft is found to be approximately 14°F; at 9,500 ft, 25°F.
A horsepower correction table, also on the back of the case, shows the amount of the correction to be applied in different horsepower ranges for variations of c.a.t. from standard conditions. This correction is added to the bhp computed on the calculator if the c.a.t. is below standard, it is subtracted when c.a.t. is above standard. When the actual c.a.t. variations do not correspond with the figures found in the 'CARB. AIR TEMP. DIFF.' table, sufficiently accurate results may be obtained by interpolation.
EXAMPLE 6. Assume the computed bhp is 660 at 12,500 ft and the c.a.t. at this altitude is 37°F, or 23°F above standard. (See Example 5.) The bhp correction in the 650-700 horsepower range is, therefore, to be subtracted. Since the c.a.t. variation from the standard, 23°F, lies between the tabulated 'CARB. AIR TEMP. DIFF'S.' of 18°F and 27°F, the horsepower correction will lie correspondingly between 12 and 18, and by interpolation is found to be approximately 15 horsepower. Subtracting the correction, the actual bhp proves to be 660 - 15 = 645.
In problems that involve computing the manifold pressure necessary to deliver a desired bhp, a c.a.t. correction is first applied to the desired bhp; the manifold pressure is then computed as it the adjusted bhp were the bhp actually desired and c.a.t. conditions were standard; but, it is essential to note, in this case the correction is subtracted from the desired bhp when the c.a.t. is below standard; and added when the c.a.t. is above.
EXAMPLE 7. It is desired to find the manifold pressure to deliver 580 bhp at 9,500 ft. and a c.a.t. of 5°F. From the standard altitude temperature table, the c.a.t. is seen from Example 5, to be approximately 20°F below standard. The horsepower correction is found by interpolation from the table to be 11 bhp, and is subtracted. The problem then resolves itself into that of computing the manifold pressure necessary to deliver 580 – 11 = 569 bhp under standard c.a.t. conditions (and whatever rpm may be specified).
Problems
The two typical problems that follow will help to illustrate the use of the power calculator.
Problem I: Find bhp, etc.
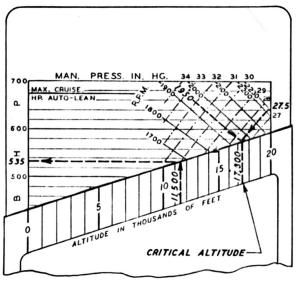
Given: R-2000 2SDG; high blower; auto-lean mixture, rpm = 1,95O; manifold pressure = 27.5 inHgA; c.a.t. = 34°F; altitude = 11,500 ft.
A. What is the bhp delivered, before and after c.a.t. correction?
B. What is the critical altitude, under standard conditions, for 1,950 rpm and 27.5 inHgA manifold pressure?
C. Is operation at full or part throttle?
D. Is the bmep limit being exceeded? Would it be exceeded at 1,600 rpm and the bhp actually delivered?
Solution I
(Hold calculator so that pressure of fingers on slide through openings will keep slide firmly against left side of case.)
A(1 ) Locate, by interpolation, the intersection of the full throttle, constant rpm and constant manifold pressure lines corresponding to the given rpm (1,950) and manifold pressure (27.5 inHgA).
A(2) Set the slide so that the sloping edge of the case passes through this intersection.
A(3) Follow the sloping edge of the case downward until the line marking the given altitude (11,500 ft) is reached.
A(4) Directly to the left of this latter point the bhp before c.a.t. correction is read from the scale as approximately 535 bhp.
A(5) The standard temperature at the given altitude (11,500 ft) is found from the table to be approximately 18°F. The given c.a.t. of 34°F is thus approximately 16°F above standard.
A(6) The correction in the 500 - 550 horsepower range is applied to the computed bhp (535), and is subtracted. It lies between the tabulated 'CARB. AIR TEMP. DIFF'S' of 9°F and 18°F, and by interpolation, the correction is found to be approximately 8 horsepower.
A(7) The actual bhp is delivered (after c.a.t. correction) is thus approximately 535 - 8 = 527 bhp.
B. The maximum or critical altitude for 1,950 rpm and 27.5 inHgA manifold pressure is determined by the altitude at which the full throttle, constant 1,950 rpm, and constant 27.5 inHgA lines intersect. It is approximately 17,300 ft.
C. Operation is at part throttle, since it lies below the full throttle, or critical altitude, for the given rpm - manifold pressure combination of 1950 rpm - 27.5 inHgA.
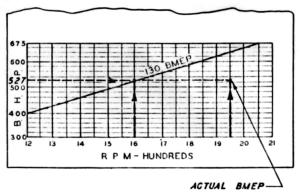
D. The bmep limit (130 psi) is not being exceeded, since the point determined on the bmep chart by the given rpm (1,950) and the actual bhp (527) is below the diagonal. It would be just barely exceeded at 1,600 rpm and 527 bhp.
 |
 |
| Problem I Parts A - C | Problem I Part D |
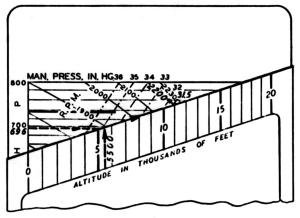
Problem II: Find manifold pressure, etc.
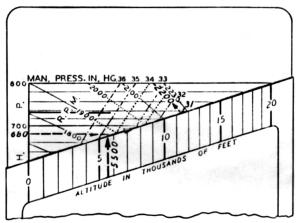
Given: R-2000 2SDG; low blower; auto-lean mixture; rpm = 2,200; bhp = 680; c.a.t. = 63°F; altitude = 5,500 ft.
A. Assuming standard conditions (i.e. making no correction for c.a.t.), what manifold pressure is required to deliver 680 bhp at the given altitude and rpm? at 2,000 rpm? at 1,900 rpm?
B. Still assuming standard conditions, is the bmep limit exceeded at any of these three rpm values? Which of these three rpm values represents the most economical operation?
C. What manifold pressure is required to deliver the desired 680 bhp at the given rpm, altitude, and c.a.t.?
Solution II
A(1) Set the slide so that the desired bhp (680) line cuts the sloping edge of the case at the given altitude (5,500 ft) mark.
A(2) Follow the sloping edge of the case upward until it intersects the full throttle, constant rpm line corresponding to the given rpm (2,200).
A(3) The manifold pressure indicated at this intersection (31 inHgA) is the one required under the given conditions.
A(4) The intersection of the sloping edge of the case with the full throttle 2,000 rpm and 1,900 rpm lines shows that manifold pressures of 32.5 inHgA and , respectively, are called for at these rpm values.
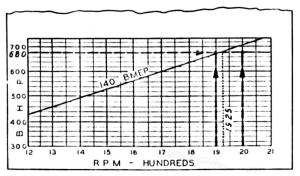
B. The 1,900 rpm - 680 bhp combination determines a point on the bmep chart that lies slightly above the diagonal line. The bmep limits are accordingly exceeded at this rpm. The rpm of 2,000 comes the nearest to the rpm for maximum economy (roughly 1,925 rpm).
C(1) The standard temperature at the given attitude (5,500 ft.) is found from the table to be approximately 40°F. The given c.a.t. of 63°F is thus approximately 23°F above standard.
C(2) The correction in the 650-700 horsepower range is applied to the desired bhp (680), and is added. It lies between the tabulated 'CARB. AIR TEMP. DIFF'S.' of 18°F and 27°F, and, by interpolation, the correction is found to be approximately 15 horsepower.
C(3) The required manifold pressure is then computed as if the desired bhp were 680 + 16 = 696 bhp, and c.a.t. were standard, the rpm and attitude remaining 2,200 rpm and 5,500 ft as given.
C(4) Applying the method outlined in A(1 – 3) above, the manifold pressure required is found to be 31.5 inHgA.
 |
 |
 |
| Problem II Part A | Problem II Part B | Problem II Part C |
Pratt & Whitney Aircraft and Wright Aeronautical Power Calculator Images
 |
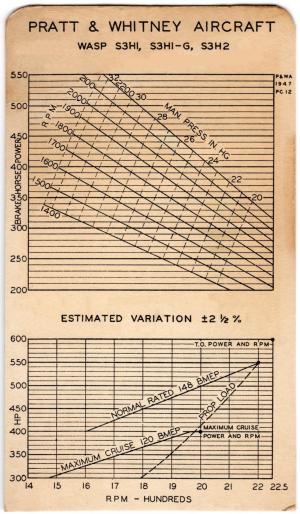 |
 |
Powered by phpBB © 2001, 2005 phpBB Group |